For over eight hundred years the façade of the church of San Nicola in Pisa has watched over a message that nobody has ever read before. Recently the front has been restored and the marble cleaned.

During the process a professor of the University of Pisa, Pietro Armienti, an expert in petrology, closely observed the circular and rectangular inlays of one of the church’s lunettes and discovered a coded message. Studying its geometry the professor realized that the symbols were an explicit reference to the findings of the first great western mathematician Leonardo Fibonacci, who was born in Pisa around 1170. Professor Armienti has just published his research report on “Journal of Cultural Heritage”.

The Church of San Nicola has a first mention in 1097. In 1297-1313 the Augustinians enlarged it probably under design by Giovanni Pisano. During the following centuries the ravages of time left its mark on the inlays of the façade making them unreadable. After its recent restoration, the message carved in the lunette of the portal has emerged with all its details, proving to be a valuable artefact which celebrates the insights that marked the birth in Pisa of a school of thought that transformed the medieval vision of the world and turned Pisa into the cradle of modern scientific thought.

What is Fibonacci Sequence?

Leonardo Bonacci (c. 1170 – c. 1250), known as Fibonacci,was an Italian mathematician, considered to be the most talented Western mathematician of the Middle Ages.

Fibonacci was born around 1170 to Guglielmo Bonacci, a wealthy Italian merchant and, by some accounts, the consul for Pisa. Guglielmo directed a trading post in Bugia, a port in the Almohad dynasty’s sultanate in North Africa. Fibonacci travelled with him as a young boy, and it was in Bugia (now Béjaïa, Algeria) that he learned about the Hindu–Arabic numeral system. Fibonacci travelled extensively around the Mediterranean coast, meeting with many merchants and learning of their systems of doing arithmetic. He soon realised the many advantages of the “Hindu-Arabic” system. In 1202 he completed the Liber Abaci (Book of Abacus or Book of Calculation) which popularized Hindu–Arabic numerals in Europe.

Liber Abaci posed, and solved, a problem involving the growth of a population of rabbits based on idealized assumptions. The solution, generation by generation, was a sequence of numbers later known as Fibonacci numbers. Although Fibonacci’s Liber Abaci contains the earliest known description of the sequence outside of India, the sequence had been noted by Indian mathematicians as early as the sixth century. In the Fibonacci sequence of numbers, each number is the sum of the previous two numbers.

Fibonacci Sequence in Nature

The Fibonacci numbers are Nature’s numbering system.

They appear everywhere in Nature, from the leaf arrangement in plants, to the pattern of the florets of a flower, the bracts of a pinecone, or the scales of a pineapple.

The Fibonacci numbers are therefore applicable to the growth of every living thing, including a single cell, a grain of wheat, a hive of bees, and even all of mankind. Plants do not know about this sequence – they just grow in the most efficient ways. Many plants show the Fibonacci numbers in the arrangement of the leaves around the stem. Some pine cones and fir cones also show the numbers, as do daisies and sunflowers.

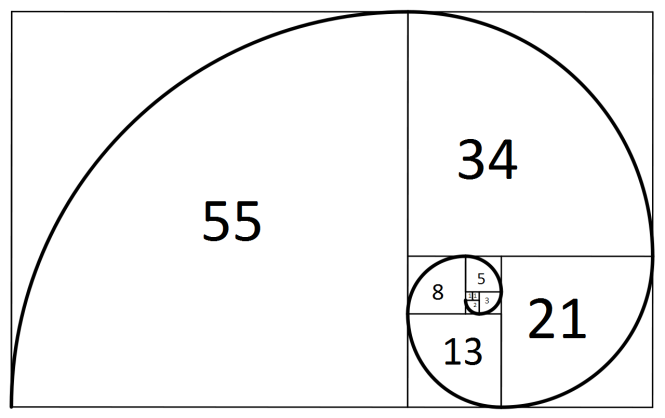
Apparently studying the diameters of the various circles one obtains the first nine elements of the Fibonacci sequence: 1,2, 3, 5, 8, 13, 21, 34 and 55. According to Professor Armienti the reference could not be more explicit and directly connects the inlay to the work of the great mathematician, or at least to a circle of his immediate colleagues or students. It appears that the inlay is an abacus which represents irrational numbers as well as made to calculate with good approximation the sides of the regular polygons inscribed in the circle with the largest diameter.
This is thus an important monument designed to instruct the elites according to the Scholastic programme. A precious gift which has been sent down to us from over eight hundred years ago and which can finally be valued.

È un richiamo esplicito alle scoperte del primo grande matematico dell’Occidente cristiano, Leonardo Fibonacci, ed è riemerso durante un recente restauro che ha riportato alla luce i marmi della Chiesa di San Nicola in via Santa Maria a Pisa.

Un originale studio del prof. Pietro Armienti, docente di Petrologia e Petrografia dell’Università di Pisa, recentemente pubblicato sul Journal of Cultural Heritage, ha permesso di interpretare le eleganti geometrie dell’intarsio della lunetta sopra l’originario portale principale come un riferimento alla celebre successione numerica individuata dal matematico pisano.
“Per secoli i segni del tempo avevano reso illeggibili gli intarsi della facciata della chiesa, la cui costruzione, che risale al XIII secolo, viene da molti attribuita a Nicola Pisano. Dopo il restauro, il messaggio scolpito nella lunetta del portale è emerso in tutti i suoi dettagli e ha permesso di dimostrare che il pregevole manufatto, che ha comportato il lavoro congiunto di matematici, teologi, artigiani, celebra le intuizioni che segnarono a Pisa la nascita di una scuola di pensiero capace di trasformare la visione medievale del mondo e di fare della città la culla della pensiero scientifico moderno.

Cos’è la sequenza di Fibonacci?

Leonardo Pisano detto il Fibonacci (1175-1250), cioè figlio di Bonaccio, individuò questa serie per la prima volta nel 1202, per risolvere un problema pratico: quante coppie di conigli si ottengono in un anno da una sola coppia supponendo che produca ogni mese (tranne il primo) una nuova coppia che a sua volta diventa fertile a partire dal secondo mese? (La risposta è 144 coppie di conigli).

Assieme al padre Guglielmo dei Bonacci, facoltoso mercante pisano e rappresentante dei mercanti della Repubblica di Pisa nella zona di Bugia in Cabilia (regione dell’odierna Algeria), passò alcuni anni in quella città, dove studiò i procedimenti aritmetici che studiosi musulmani stavano diffondendo nelle varie parti del mondo arabo. Qui ebbe anche precoci contatti con il mondo dei mercanti e apprese tecniche matematiche sconosciute in Occidente. Alcuni di tali procedimenti erano stati introdotti per la prima volta dagli indiani, portatori di una cultura molto diversa da quella mediterranea. Proprio per perfezionare queste conoscenze Fibonacci viaggiò molto, arrivando a Costantinopoli, alternando il commercio con gli studi matematici. Molto dovette ai trattati di Muhammad ibn Musa al-Khwarizmi, Abu Kamil e ai maestri arabi, senza però essere mero diffusore della loro opera. Ritornato in Italia, la sua notorietà giunse anche alla corte dell’imperatore Federico II, soprattutto dopo aver risolto alcuni problemi del matematico di corte. Per questo motivo gli fu assegnato un vitalizio che gli permise di dedicarsi completamente ai suoi studi.

Nel 1202 pubblicò, e nel 1228 riscrisse (lo fece pubblicare solo dopo la sua morte però, lasciandolo nel suo testamento) il Liber abbaci, opera in quindici capitoli con la quale introdusse per la prima volta in Europa (nel capitolo I) le nove cifre, da lui definite “indiane”, e il segno 0 che in latino è chiamato zephirus, adattamento dell’arabo sifr, ripreso a sua volta dal termine sanscrito śūnya, che significa “vuoto”. Zephirus in veneziano divenne zevero ed infine comparve l’italiano “zero”. Per mostrare ad oculum l’utilità del nuovo sistema egli pose sotto gli occhi del lettore una tabella comparativa di numeri scritti nei due sistemi, romano e indiano. Fibonacci espose così per la prima volta in Europa la numerazione posizionale indiana (adottata poi dagli arabi). All’epoca il mondo occidentale usava i numeri romani e il sistema di numerazione greco e i calcoli si eseguivano con l’abaco. Questo nuovo sistema stentò molto ad essere accettato, tanto che nel 1280 la città di Firenze proibì l’uso delle cifre arabe da parte dei banchieri. Si riteneva infatti che lo “0” apportasse confusione e venisse impiegato anche per mandare messaggi segreti e, poiché questo sistema di numerazione veniva chiamato “cifra”, da tale denominazione deriva l’espressione “messaggio cifrato”.

Nella successione di Fibonacci ogni numero è il risultato della somma dei due precedenti: 0, 1, 1, 2, 3, 5, 8, 13… fino all’infinito. Fino al XIX secolo a questa successione non fu attribuita alcuna importanza, finché si scoprì che può essere applicata, per esempio, nel calcolo delle probabilità, nella sezione aurea e nel triangolo aureo.

I numeri di Fibonacci si trovano anche in natura, per esempio nella disposizione delle foglie.

In molti alberi, scegliendo una foglia su uno stelo e assegnandole il numero “0”, contando il numero di foglie fino ad arrivare a una perfettamente allineata con la foglia “0”, probabilmente si troverà un numero di Fibonacci. Anche i petali di moltissimi fiori sono un numero di Fibonacci.

Secondo l’interpretazione del professor Armienti, le eleganti simmetrie dell’opera sono un richiamo diretto alle scoperte del matematico pisano: “Se si assume come unitario il diametro dei cerchi più piccoli dell’intarsio, i più grandi hanno diametro doppio, i successivi triplo, mentre quelli di diametro 5 sono divisi in spicchi nei quadratini ai vertici del quadrato in cui è inscritto il cerchio principale, quello centrale ha diametro 13 mentre il cerchio che circoscrive i quadratini negli angoli ha diametro 8. Gli altri elementi dell’intarsio disposti secondo tracce circolari individuano circonferenze di raggio 21 e 34, infine il cerchio che circoscrive l’intarsio ha diametro 55 volte più grande del circolo minore. 1,2,3,5,8,13,21,34,55 sono i primi nove elementi della successione di Fibonacci”.

Per Armienti, il riferimento non potrebbe essere più esplicito e collega direttamente l’intarsio all’opera del grande matematico o a una cerchia di suoi diretti collaboratori o allievi. L’intarsio di fatto è un abaco per rappresentare numeri irrazionali come p o il rapporto Aureo f, oltre che per calcolare con un’ottima approssimazione i lati dei poligoni regolari inscritti nel cerchio diametro maggiore. Si tratta dunque di un importante monumento la cui presenza era stata concepita per l’educazione delle élites, secondo il programma della filosofia scolastica: un dono prezioso della sapienza degli antichi giunto dopo ottocento anni di oblio.